The leaves are important sites for plants to carry out photosynthetic, transpiration and respiration, and they are also the main organs for making nutrients. The size of leaf area, leaf structure and function are important indicators of plant growth and nutritional status. In the production practice, the size of the leaf area is an important basis for formulating cultivation patterns and fertilization schemes. Therefore, it is very important to establish a convenient and accurate leaf area determination method.
The method for determining the leaf area mainly includes square count method, leaf area instrument method, regression equation method, drawing paper weighing method, planimeter method, direct weighing method, digital image processing method, and the like, but due to different plant The leaf morphology is quite different, so the appropriate methods for determining the leaf area of ​​different plants are different. In this paper, the application of four methods in the determination of the leaf area of ​​E. grandis was comparatively studied with the leaves of E. urophylla as the material, aiming to find an accurate, rapid and economical method for the determination of E. grandis leaf area.
1 Materials and Methods 1.1 Materials The test material Dayejing was collected from Tianhe County of Chongzuo City in September 2010. The height of the tree is about 6m. Normal mature leaves were randomly picked from the east, south, west and north directions of the canopy. 52 sheets, each blade number, in order to facilitate the record.
1.2 Measurement method 1.2.1 Instrument method Use the AM-300 portable leaf area meter to measure the size of each leaf, record the area value of each leaf, and measure the chlorophyll content using the chlorophyll detector.
1.2.2 The grid method describes the outline of the blade on a 1 mm × 1 mm minimum square grid, and counts the number of squares occupied by the outline of the leaves. The number of squares that meet or exceed the half grid is less than half a square. Go, statistics each leaf area of ​​square paper.
1.2.3 Coefficient Method Using a ruler to measure the length of each leaf (from the leaf base to the tip, not including the petiole) and leaf width (the widest point in the vertical direction of the leaflet and the main vein), determine the length and width product. The ratio of the area measured by the laser leaf area meter to the length and breadth product of the leaf was calculated by dividing the number of blades of each layout number by the ratio of the area to the product of length and breadth, that is, the “coefficientâ€. The average value of the leaf coefficient was used as the coefficient, and was recorded as C. Multiply the long-width product of each blade by C to obtain the leaf area estimated by the coefficient method for each blade.
1.2.4 Regression analysis method Using a ruler to measure the leaf length and leaf width of each leaf, leaf length, leaf width, leaf length × leaf width were taken as independent variables, respectively recorded as l, w, lw, with laser leaf area The leaf area measured by the instrument is the dependent variable, denoted as y, and the linear regression equation y=a+bx for the area-length product is obtained. Substituting the prepared independent variables into the corresponding linear regression equations, the leaf area measured by the area-to-length-long product linear regression estimation method was obtained.
1.3 Data Statistical Analysis Data obtained from the four methods were analyzed for statistical differences using SPASS and EXCEL statistical software.
2 Results and analysis 2.1 Leaf shape characteristics of big leafhopper Leaf length, leaf width, leaf area, and leaf shape index (length/width) can accurately reflect the shape of the entire leaf of the plant, and can be used as an important method to accurately distinguish and identify leaf shape. Characteristic Parameters. From Table 1, it can be concluded that the standard error of the leaf blade index is 0.083. Compared with the leaf index, the leaf shape index can accurately reflect the leaf shape characteristics of the leafhopper. The leaf blade index of the leafhopper was 2.586, indicating that the leaf shape was narrow and long.

Table 1 Leaf traits of Begonia macrophylla 2.2 Comparison of the determination results of different leaf area can be seen in Table 2. There was a significant difference in the leaf area of ​​Begonia macrophylla measured by the four methods (P<0.05). There are significant differences between the measured value of the coefficient method and the leaf area measurement value of the grid method. There is a significant difference in the leaf area measured by the grid method and the regression analysis method. The measured value of the regression method and the leaf area determined by the instrument method are not Significant difference.
As can be seen from Table 3, the variation in the coefficient of variation for each method of leaf area determination is not significant. The smaller coefficient of variation indicates that the method for measuring leaf area is more accurate than other methods. As a result, the coefficient of variation of the large leafhopper measured by regression analysis was the smallest, indicating that the regression analysis method was more accurate in determining the leaf area of ​​the leafhopper. It can also be seen that the standard deviation measured by the regression analysis method is relatively small at 35.727, and the leaf area changes within a relatively concentrated range, while the leaf area changes determined by the other three methods are relatively wide.

Table 2 Comparison of Average Leaf Area Measured by Several Measurement Methods

Table 3 Standard deviations and coefficient of variation of several measurement methods 2.3 Regression equation and test of leaf area of ​​Eucalyptus grandis Table 4 can be seen: leaf length, leaf width, leaf length × leaf width and leaf area have extremely significant correlation Sex. The correlation coefficient R of each regression equation was in the range of 0.9636~0.9970, showing a very significant positive correlation. The correlation coefficient r value of the regression equation with leaf length @ leaf width as the largest variable is 0.9970, and the correlation coefficient r value of the regression equation with leaf length as the variable is the smallest with 0.9760.
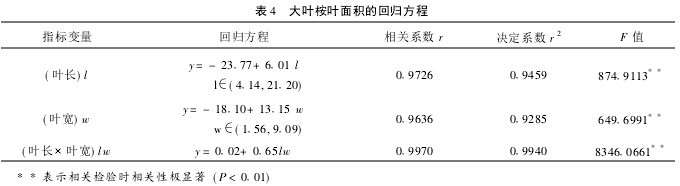
Table 4: Regression Equations for Leaf Area of ​​the Large-leaved Buckwheat. 3 Conclusion The leaf area was estimated by using the power function regression equation to determine the leaf width of 4 clones of Populus tomentosa. The results of this paper show that there are significant differences in leaf area measurements between different methods. The accuracy from high to low is: regression analysis, leaf area instrument method, grid count method and coefficient method. In the regression analysis test, a one-line linear regression equation established with leaf length, leaf width, and leaf length @ leaf width as independent variables has a correlation coefficient as high as 0.9636 or more, which is highly significant positive correlation with leaf area and can be used to measure large Leafhopper leaf area. Among them, the regression coefficient with leaf length @ leaf width as the independent variable is the largest, so this equation can be used as the best method for the leaf area of ​​the big leaf.
The regression equation is used to calculate the leaf area of ​​A. macrophylla. It can be measured in vivo in production practice. It only needs to measure leaf width and leaf length. This method is simple, fast, and has no damage to leaves.
Starter Motor Generator,Starter Parts,Starter Assembly
Bison Machinery Co., Ltd , http://www.zjengine.com